蒙特卡洛树搜索(Monte Carlo Tree Search)
也叫 MCTS,早有耳闻的算法,结果今天花了十几分钟就理解原理了,原理好简单,但效果好强大。
MTCS的根基 - 蒙特卡洛方法
注意!这和 蒙特卡洛树搜索 不是同一种算法,很多科普文章都搞混了这两个概念,声称 AlphaGO 使用的是蒙特卡洛方法。
蒙特卡洛法方法 是什么呢,它是评判棋盘局面的一种方法,我们上面说到,围棋很难写出好的估值函数,于是上世纪有人提出了一种神奇的方法:双方在某个局面下「随机」走子,注意是「随机」走,走到终局或者残局为止,随机很多次(比如一万盘),计算胜率,胜率越高的局面就越好。
但其实这是个伪算法,就举个极端的例子,比如说我下某步棋之后,对方有 100 种应对—— 99 种会导致劣势,但是有 1 种必胜下法,我就绝对不能下这步棋。
但是「蒙特卡洛树搜索」是个真算法,并且它其实在 alphago 之前早就有了,而且能胜业余的段级选手,在当时是很大的突破。
基本概念
蒙特卡洛树搜索(简称 MCTS)是 Rémi Coulom 在 2006 年在它的围棋人机对战引擎 「Crazy Stone」中首次发明并使用的的 ,并且取得了很好的效果。 我们先讲讲它用的原始 MCTS 算法(ALphago 有部分改进),蒙特卡洛树搜索,首先它肯定是棵搜索树
我们回想一下我们下棋时的思维——并没有在脑海里面把所有可能列出来,而是根据「棋感」在脑海里大致筛选出了几种「最可能」的走法,然后再想走了这几种走法之后对手「最可能」的走法,然后再想自己接下来「最可能」的走法。这其实就是 MCTS 算法的设计思路。
它经历下面 3 个过程(重复千千万万次)
- 选择(Selection)
- 扩展 (expansion)
- 模拟(Simulation)
- 回溯(Backpropagation)
这四个概念有点难,我们不按顺序解释这 4 个概念。
模拟(Simulation)
我们不按顺序,先讲模拟,模拟借鉴了我们上面说的蒙特卡洛方法,快速走子,只走一盘,分出个胜负。 我们每个节点(每个节点代表每个不同的局面)都有两个值,代表这个节点以及它的子节点模拟的次数和赢的次数,比如模拟了 10 次,赢了 4 盘,记为 4/10。 我们再看多一次这幅图,如图,每个节点都会标上这两个值。
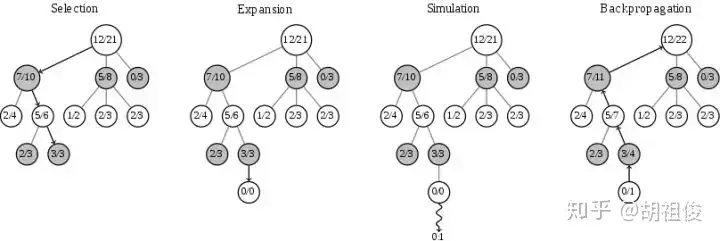
选择(Selection)
我们将节点分成三类:
- 未访问:还没有评估过当前局面
- 未完全展开:被评估过至少一次,但是子节点(下一步的局面)没有被全部访问过,可以进一步扩展
- 完全展开:子节点被全部访问过 我们找到目前认为「最有可能会走到的」一个未被评估的局面(双方都很聪明的情况下),并且选择它。

什么节点最有可能走到呢?最直观的想法是直接看节点的胜率(赢的次数/访问次数),哪个节点最大选择哪个,但是这样是不行的!因为如果一开始在某个节点进行模拟的时候,尽管这个节点不怎么好,但是一开始随机走子的时候赢了一盘,就会一直走这个节点了。 因此人们造了一个函数
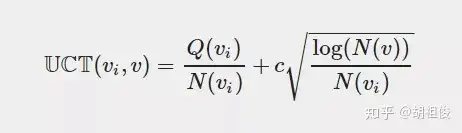
Q(v) 是该节点赢的次数,N(v) 是该节点模拟的次数,C 是一个常数。 因此我们每次选择的过程如下——从根节点出发,遵循最大最小原则,每次选择己方 UCT 值最优的一个节点,向下搜索,直到找到一个 「未完全展开的节点」,根据我们上面的定义,未完全展开的节点一定有未访问的子节点,随便选一个进行扩展。 这个公式虽然我们造不出来,但是我们可以观赏它的巧妙之处,首先加号的前面部分就是我们刚刚说的胜率,然后加号的后面部分函数长这样:
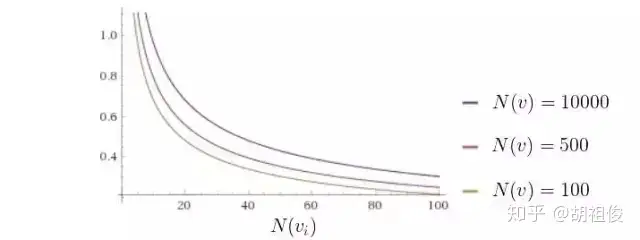
随着访问次数的增加,加号后面的值越来越小,因此我们的选择会更加倾向于选择那些还没怎么被统计过的节点,避免了我们刚刚说的蒙特卡洛树搜索会碰到的陷阱——一开始走了歪路。
扩展(expansion)
将刚刚选择的节点加上一个统计信息为「0/0」的节点,然后进入下一步模拟(Simluation)
回溯(Backpropagation)
Backpropagation 很多资料翻译成反向传播,不过我觉得其实极其类似于递归里的回溯,就是从子节点开始,沿着刚刚向下的路径往回走,沿途更新各个父节点的统计信息。

再放一次这个图,可以观察一下在模拟过后,新的 0/0 节点,比如这里模拟输了,变成了 0/1,然后它的到根节点上的节点的统计信息的访问次数全部加 1,赢的次数不变。
实现伪代码
def monte_carlo_tree_search(root):
while resources_left(time, computational power):
leaf = traverse(root) # leaf = unvisited node
simulation_result = rollout(leaf)
backpropagate(leaf, simulation_result)
return best_child(root)
def traverse(node):
while fully_expanded(node):
node = best_uct(node)
return pick_univisted(node.children) or node # in case no children are present / node is terminal
def rollout(node):
while non_terminal(node):
node = rollout_policy(node)
return result(node)
def rollout_policy(node):
return pick_random(node.children)
def backpropagate(node, result):
if is_root(node) return
node.stats = update_stats(node, result)
backpropagate(node.parent)
def best_child(node):
pick child with highest number of visits
算法什么时候可以终止
取决于你什么时候想让他停止,比如说你可以设定一个时间,比如五秒后停止计算。 一般来说最佳走法就是具有最高访问次数的节点,这点可能稍微有点反直觉。这样评估的原因是因为蒙特卡洛树搜索算法的核心就是,越优秀的节点,越有可能走,反过来就是,走得越多的节点,越优秀。
alpha狗狗到底改进了什么,使得它变成了世界最佳?
deepmind 将 MCTS 和近年来取得突破性进展的神经网络结合起来,主要是针对上面两个步骤作了改进:
1. 模拟: 首先上面四步里,最玄学、感觉最不靠谱的一步是「模拟」,用随机快速走子的方法走完一盘棋,然后记录胜盘和下了多少盘,这一步虽然是蒙特卡洛树搜索的核心,但是并不那么准确。 在 alphago Lee 中,叶子节点的估值是两个部分的加权和:
- 一种带有手工特征的浅层 softmax 神经网络:采用自定义快速走棋策略的标准走棋评估
- 估值网络:基于 13 层卷积神经网络的位置评估,训练自 Alpha Go 自我对弈的三千万个不同位置(没有任何两个点来自同一场游戏) 而 alphago zero 迈出了更远的一步,他们根本就不进行模拟,而是用一个 19 层 CNN 残差神经网络直接评估当前节点。(神经网络可以输出位置评估,得出每个位置的概率向量) 也就是说,利用神经网络,无需模拟,直接能算出每个位置的概率,可以说是直接消除了玄学问题。
2. 选择: 既然已经不是真的通过「模拟」的出赢的次数和已经评估的次数,那么我们之前通过 UCT 值的大小来向下搜索、选择一个未访问的叶子节点的方法也需要作出相应修改。 函数变为:
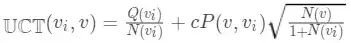
其中 UCT(v_i, v) 表示从状态(节点) v_i 转移到 v 的价值评估,P(v_i, v)表示从状态 v_i 转移到 v 的概率,或者用一个术语叫做「移动的先验概率」,这个概率是用策略网络训练出来的,基于人类游戏数据集的受监督学习。 有趣的是,在 Deepmind 的蒙特卡洛树搜索变种里,由于监督学习策略网络在实际中表现更好,因此它的结果被用来估测行动先验概率)。那么强化学习策略网络的目的是生成 3 千万位置数据集,用于训练估值网络(估值网络就是我们上一步说的用来替代「模拟」的网络)。 而在 Alphago Zero 中只有一个网络,它既是估值网络也是策略网络。它完全通过从随机初始状态开始进行自我对弈训练。并行训练多个网络,在每个检查点,基于当前最优的神经网络,评选出最优的网络用来生成训练数据。